技术美术百人计划学习笔记(图形1.1-1.4)
因为前两章基础概念较多,所以放在一起整理了
渲染流水线
如图:
数学基础
向量运算
认识向量
向量的定义
- 向量是有大小和方向的有向线段,没有位置只有大小和方向
- 向量的箭头是向量的结束,尾是向量的开始
- 向量描述的位移能够被认为是与轴平行的位移序列
向量与标量
- 向量:有大小、有方向
- 标量:有大小,没方向
向量与点
- 向量与点数学形式上相同,但几何意义完全不同
- 点:有位置,没有实际的大小和方向
- 向量:无位置,有实际的大小和方向
- 联系:任何一个点可以看作是从原点出发的向量
零向量
- 零向量是唯一大小为零的向量
- 零向量是唯一一个没有方向的向量
- 零向量不是一个点
- 零向量表示的是没有位移,如同零标量表示没有数量一样
向量的计算
向量与标量
- 没有加法与减法
- 乘法:将每个分量都与标量相乘
- 除法:等同于乘以标量的倒数
- 乘除的几何意义:以标量的大小缩放向量的长度,负值则方向相反(将向量缩放至k个标量单位)
向量的模长
表示向量的长度,为向量x和y的算术平方根
标准化向量
用于只需要知道方向,不关心大小的向量。例如:法线
向量与向量的加减法
三角形法则、四边形法则
计算两点间距离
向量相减计算得到位移向量,位移向量的模长即为两点之间的距离
向量的点积运算
- 向量点乘就是分量乘积的和,结果是一个标量并满足交换律
点积的几何意义
点乘的结果描述了两个向量的相似程度,点乘值越大,夹角角度越小,两个向量越接近
向量投影
向量a在向量b上的投影为
点积的应用:Lambert光照模型
最简单通用的模拟漫反射的光照模型
向量的叉积
几何意义:判断一个点是否在三角形内
作业
向量各方面的几何意义:
- 向量(a,b):表示从坐标系原点指向点(a,b)的向量
- 向量(a,b)乘标量:表示向量的放大缩小,标量为负则向量方向取反
- 向量点乘:①用于计算投影;②单位向量点乘用于表示两条向量之间夹角的大小;③向量点乘自己后取平方根获得向量模长
- 向量叉乘:①用于判断点是否在三角形内部;②根据两条不平行的向量,叉乘计算出与两条向量共同所在平面垂直的向量,例如Billboarding效果
矩阵运算
矩阵变换的几何意义:得到点在新的坐标系下的位置

特殊的矩阵
- 方阵
- 单位矩阵
- 零矩阵
矩阵的计算
矩阵的加减法
几何意义:对单位向量的变换,新得到的单位向量就是将两个矩阵相加分别得到的列向量
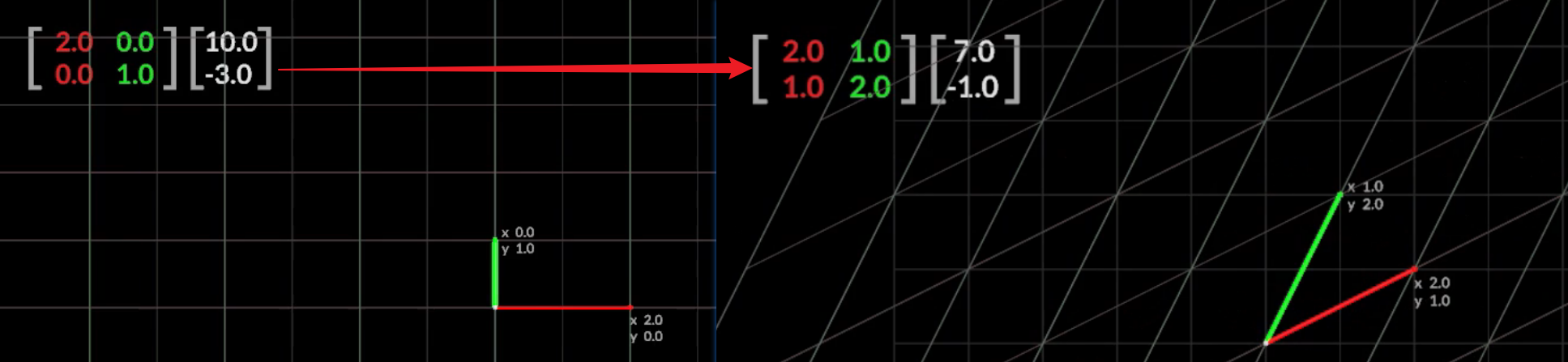
矩阵的数乘
几何意义:对空间的缩放

矩阵相乘
几何意义:可以用点积来方便记忆
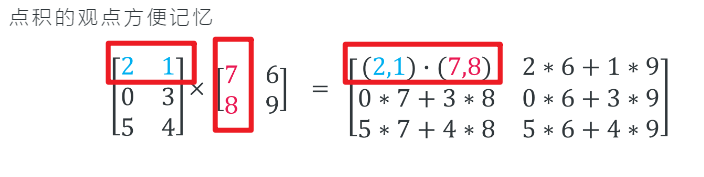
几何意义:
-
矩阵乘矩阵,计算得到矩阵
进行矩阵变换,更改单位向量(转换到新的坐标系)
-
矩阵乘列向量,计算得到向量或坐标
注意:矩阵相乘不满足交换律,按照变换顺序,矩阵从右往左进行计算。但是满足结合律,进行复合变换可以先将所有矩阵相乘,再去乘向量
矩阵的仿射变换
在Unity、Houdini的矩阵存储不同于图形学案例,他们采用的是列优先存储,所以矩阵的平移变换可能在最后一行,而非最后一列,(需要转置)
详细的各个放射变化见Games101的笔记
MVP矩阵
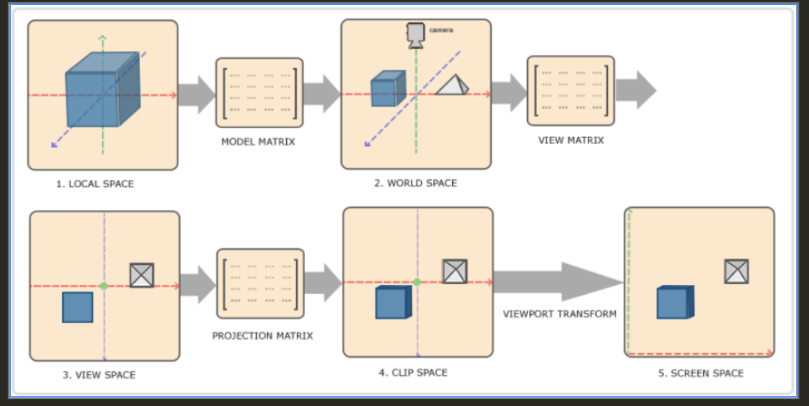
Model矩阵
模型空间→世界空间
- 模型空间:以自身为中心的空间坐标系
- 世界空间:以世界为中心的空间坐标系
缩放→旋转→平移依次进行矩阵变换

View矩阵
世界空间→视觉空间
- 视觉空间:以摄像机为原点的空间坐标系
先求V矩阵的逆矩阵(视觉空间→世界空间),再对他进行逆变换得到V矩阵
Perspective矩阵
- 不是真正的投影,只是为投影做准备
- 目的:判断顶点是否在可见范围内
- P矩阵:对x,y,z分量进行缩放,用w分量做范围值。如果x,y,z都在w范围内,那该点在裁剪空间内。
作业
模型空间世界空间视野空间的区别在于空间坐标系的原点不同,模型空间的空间坐标系原点是物体在创建时所确定的中心,世界空间的空间坐标系原点是世界中心,视野空间的空间坐标系原点是摄像机。
P矩阵推导见Games101笔记
纹理基础
纹理是什么
一张图片 一种可供着色器读写的结构化存储形式
一张纹理对象除了保存一些图片信息外,还会储存一些纹理采样的设置

纹理管线
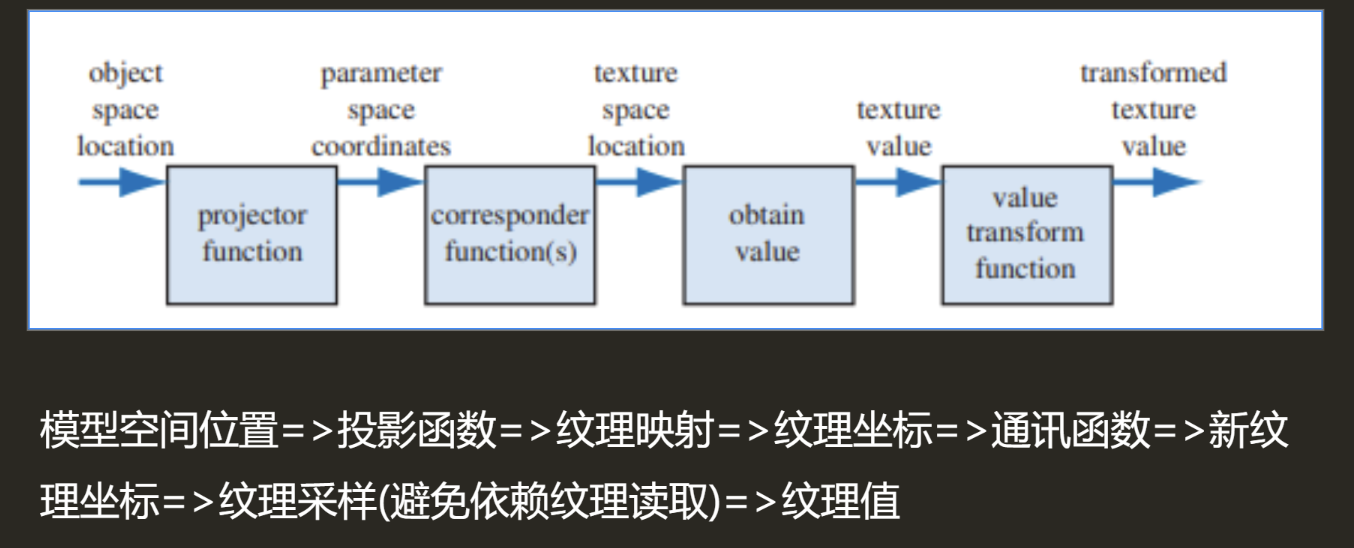
- 投影函数:获取我们要渲染的位置,将它从模型空间投影到纹理空间中,转化为UV坐标(投影指的是纹理投影,不同于摄像机投影,常规情况下投影函数通常会在“展UV”的阶段中使用,将投影的结果存储在顶点数据中。所以通常我们是直接使用存储在模型顶点数据中的投影的结果)
- 通讯函数:将UV坐标进行一个灵活的扩展,实现平移缩放旋转或者是控制图像的应用方式等等,得到一个新的纹理坐标,用这个纹理坐标就可以去获取纹理的值了(纹理采样)
- 着色器中的纹理通常会以Sampler Variable(采样器变量)的形式存在,即我们经常看见的sampler,这是一种Uniform类型的变量,在处理不同片元时这个变量是不变的。
- 依赖纹理读取:当我们使用tex2D或类似方式去访问纹理时,只要fragment shader不是直接用vertex shader传过来的数据,而是需要计算的数据,那么他就会产生一个叫做依赖纹理读取的东西,哪怕这个处理只是简单的交换UV的两个坐标。只要不是顶点着色器传过来的纹理采样数据,在片元着色器需要计算纹理偏移,哪怕是只进行了一些计算,也会影响性能的表现。
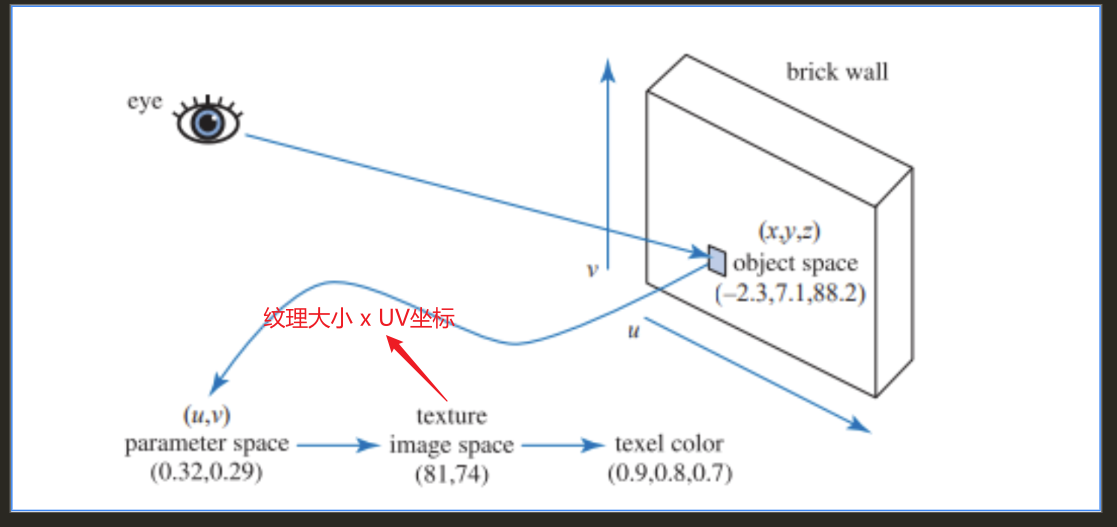
-
后续获取一个具体纹素的颜色值就要看纹理采样的设置来决定了(采样设置包含在一个纹理对象中)
-
纹理采样设置之Wrap Mode
决定UV值在[0,1]之外的表现

-
纹理采样设置之Filter Mode
- 纹理放大:
描述不同形状大小角度缩放比的情况下我们应该如何应用纹理让他的采样更加合理(纹理过滤可在硬件中完成,也可在软件中完成,也可在软件和硬件中共同完成)

Nearest Neighbor:获取最邻近点(采样一次),获得像素化的表现,消耗很省
Bilinear Interpolation:双线性插值(采样四次)

Cubic Convolution:立方卷积插值(采样16次)

光滑曲线插值:在2x2纹理组之间进行插值(采样四次)
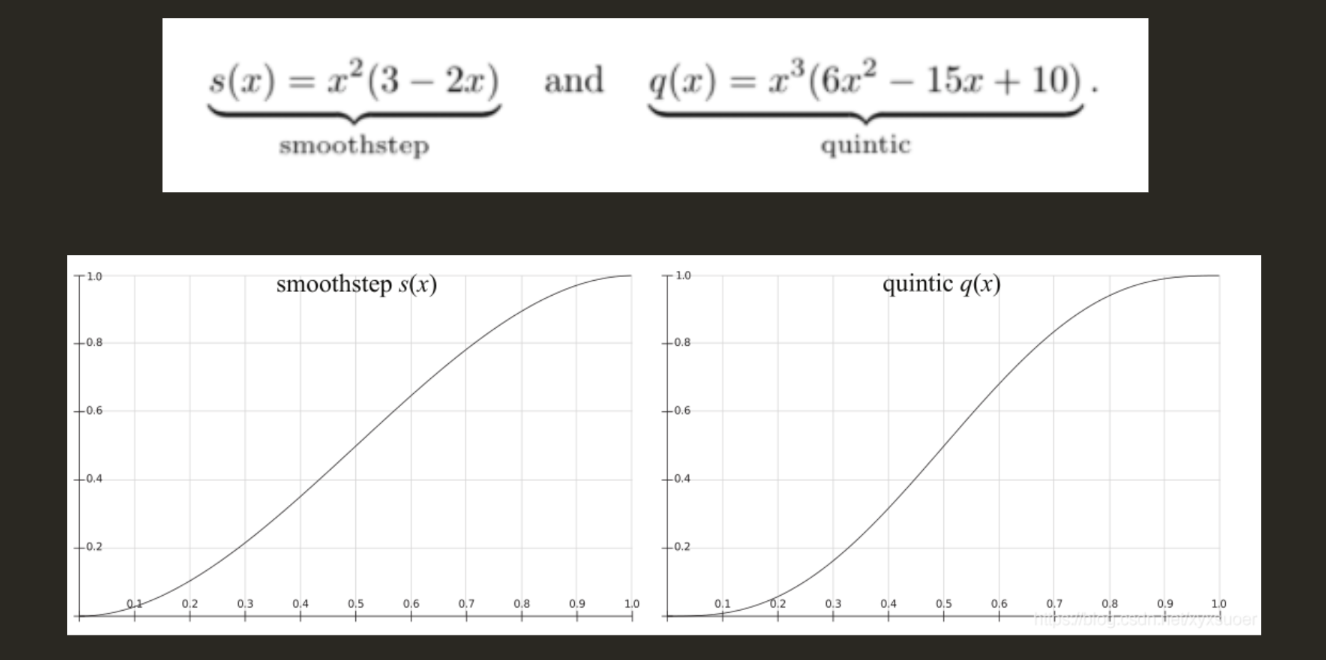
与双线性插值很相似,区别在于在将UV坐标带入读取纹理前多加了一步对UV坐标的处理

效果对比:
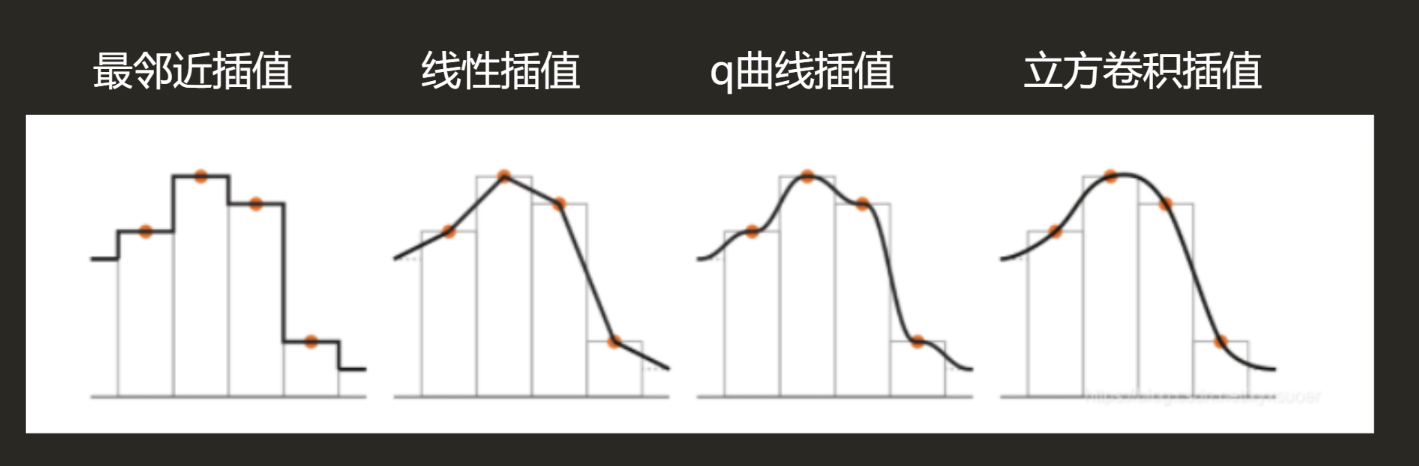
- 纹理缩小
常见方法是最邻近与双线性插值:

Mipmap:预处理纹理并创建数据结构,有助于实时工作时快速计算一组纹素对一个像素的近似值,且内存比原本多了1/3
如何正确选择Mipmap level:使用四个像素单元格所形成的一个四边形的最长边来近似这个像素覆盖的范围(显卡执行pixel是将其都分成2x2的一组,然后分块并行执行的→用于计算ddx和ddy,四个一组的pixel块是共享偏导值的)
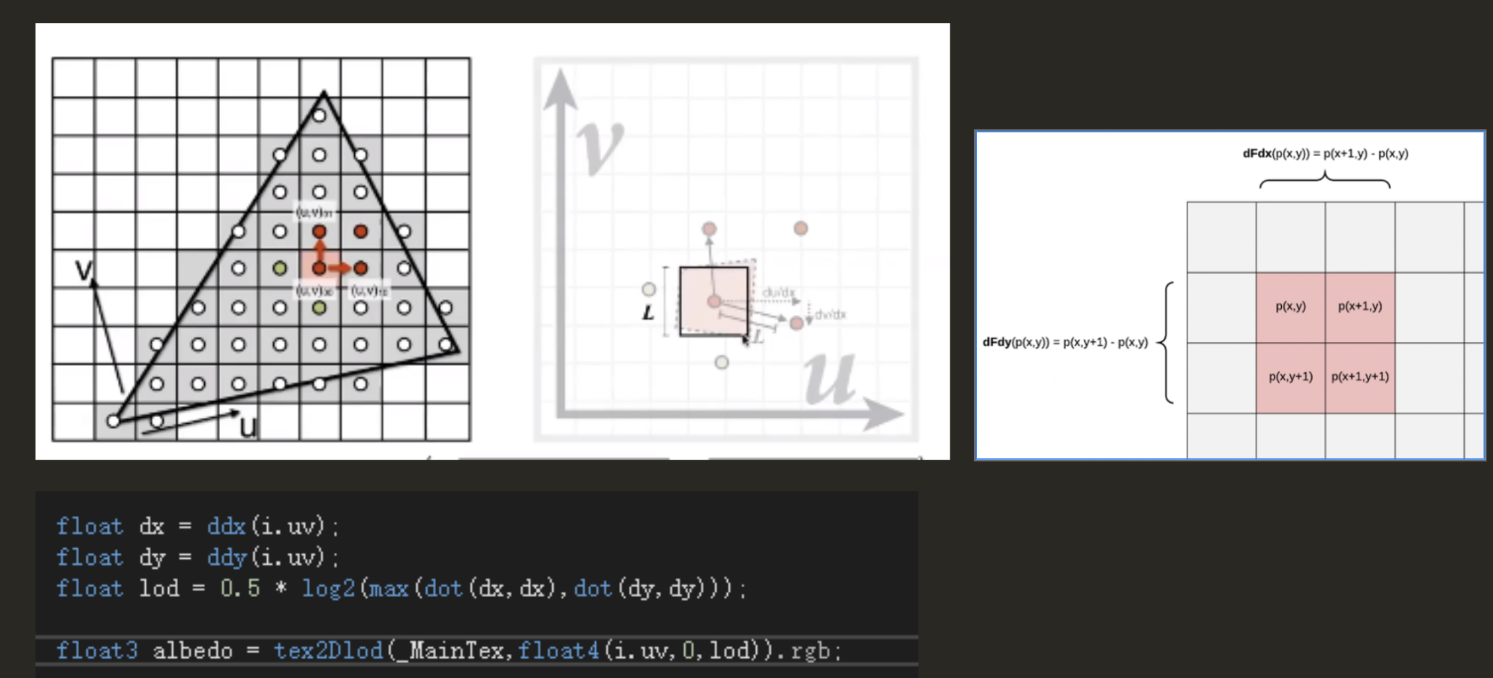
Bilinear Interpolation:三线性插值,在两个Mipmap之间再进行一次插值
但是Mipmap催在overblur的问题,只能用于各向同性贴图
Ripmap:各向异性过滤Anisotropic Filtering的一种方法,但是还是存在overblur;还有EWA过滤,用椭圆的方式存储纹素,效果好但是开销大

-
纹理优化
CPU渲染优化常见方式——纹理图集/数组
减少Draw Call,避免渲染时频繁改变纹理带来的消耗

GPU渲染常见方式——纹理压缩
从带宽入手,显存带宽指GPU独显的专用内存的速度,如果游戏速度受限于显存带宽的话,往往是我们所使用的纹理实在太大,GPU它没有办法快速处理
-
减少了资源在CPU中进行解压缩的过程
-
减小了包体大小,减少了数据量级,减轻了带宽计算的压力
-
内存的使用效率更高
纹理应用
立方体贴图CubeMap

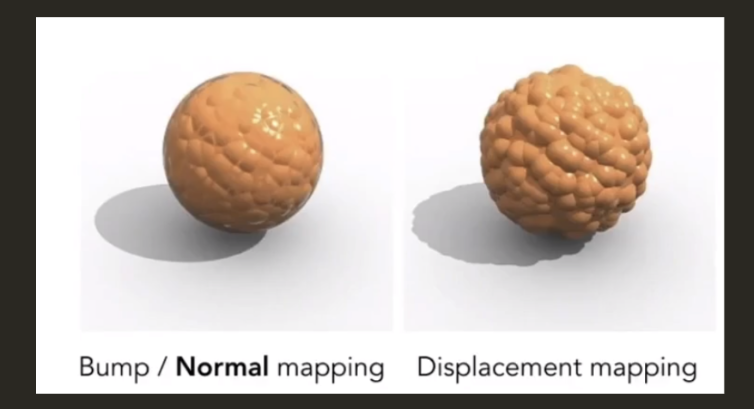
凹凸贴图Bump Mapping
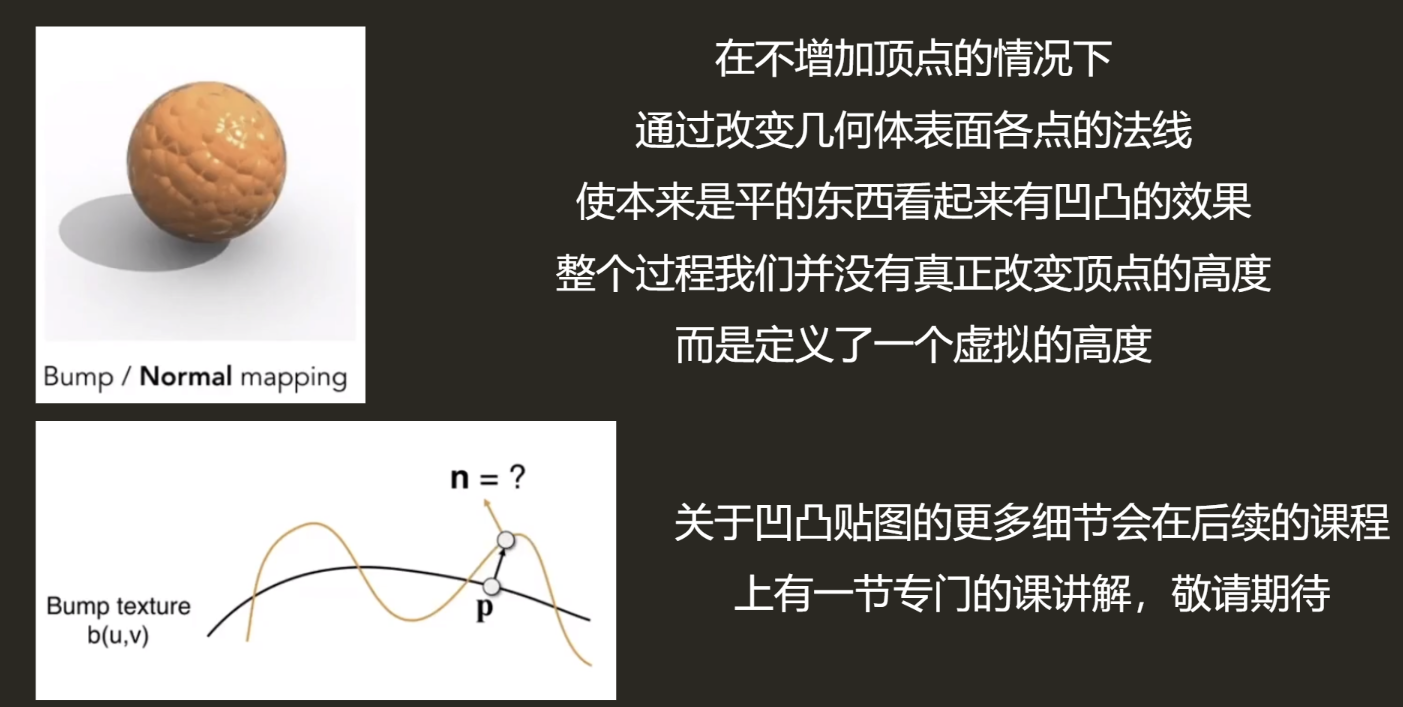
位移贴图Displacement Mapping
凹凸贴图是模拟,而位移贴图是真的把顶点做了位置的移动
作业
Filter Mode有几种?
- Nearest Neighbor最邻近(采样一次)
- Bilinea Interpola双线性插值(采样4次)
- Cubic Convolution立方卷积插值(采样16次)
- Lanczos Interpolation兰索斯插值(采样64次)
- Qu´ılez光滑曲线插值(采样4次)
纹理贴图的优化方式及原理?
- 使用Texture atlas纹理图集或纹理数组,减少Draw Call次数,减少切换渲染状态的次数来进行CPU方向的优化
- 对纹理进行压缩,减轻显存带宽计算的压力
主流平台API介绍
API的定义
是一个图形库,用于渲染2D、3D矢量图形的跨语言、跨平台的应用程序编程接口(API),针对GPU
基础概念
应用端:我们自己的程序端,相对于OpenGL ES,我们属于应用端
图元:要渲染的几何物体,或者形状
纹理:通俗点可以理解为一张图片
纹素:纹理的基础单元,不同于像素(不是一个维度的东西)
顶点数组:顶点指的是组成图元的各个顶点的属性,这些属性可以一起存到一个内存数组中
顶点缓冲区:在显存中专门分配一块显存来存储这个顶点数组,这个显存就被称为顶点缓冲区
顶点着色器、片元着色器:跑在GPU上的程序片段
主流图形API
手机:ios和Android都支持OpenGL ES
电脑:Windows支持DX和OpenGL,Linux/Mac(Unix)支持OpenGL
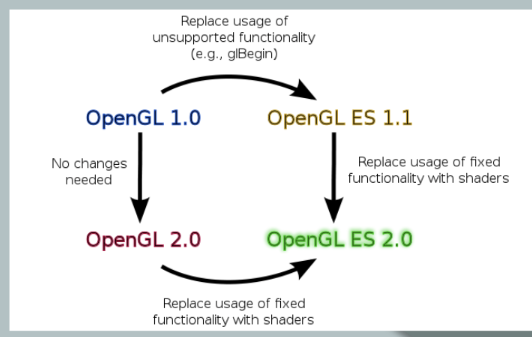
OpenGL ES
相同点:
相比于 OpenGL ES 1.x 系列的固定功能管线,OpenGL ES 2.0 和 OpenGL ES 3.0 都是可编程图形管线。开发者可以自己编写图形管线中的 顶点着色器 和 片段着色器 两个阶段的代码。
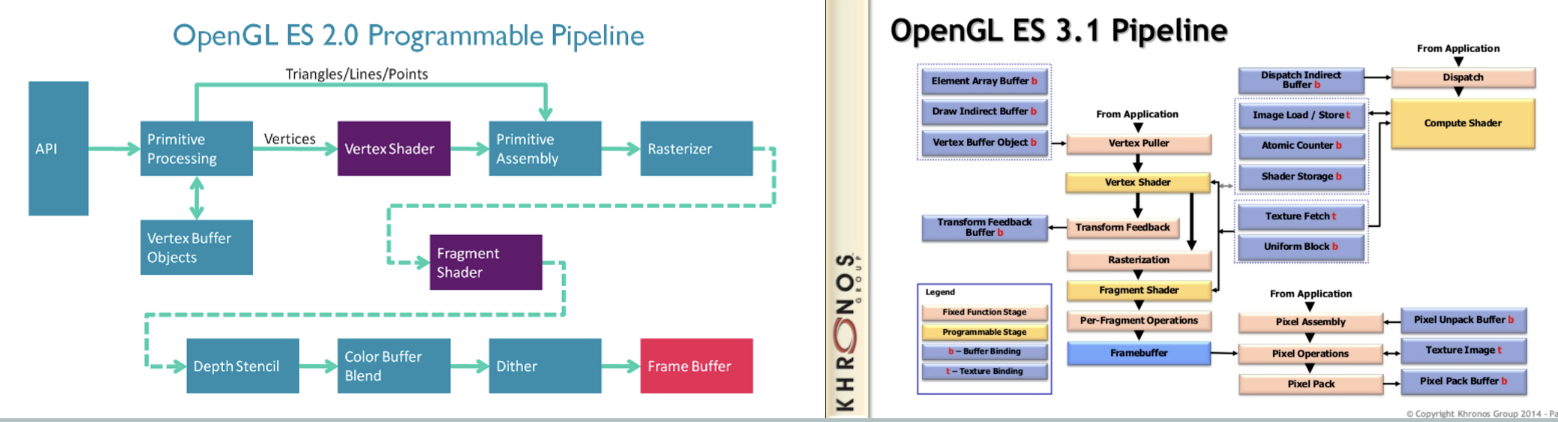
不同点:
-
兼容性:向后兼容
-
新特性:3.0引入采用阴影贴图、体渲染、基于GPU的粒子动画、几何形状实例化、纹理压缩和伽马矫正等新技术
-
渲染管线:3.0移除了Alpha Test和逻辑操作LogicOp两部分
-
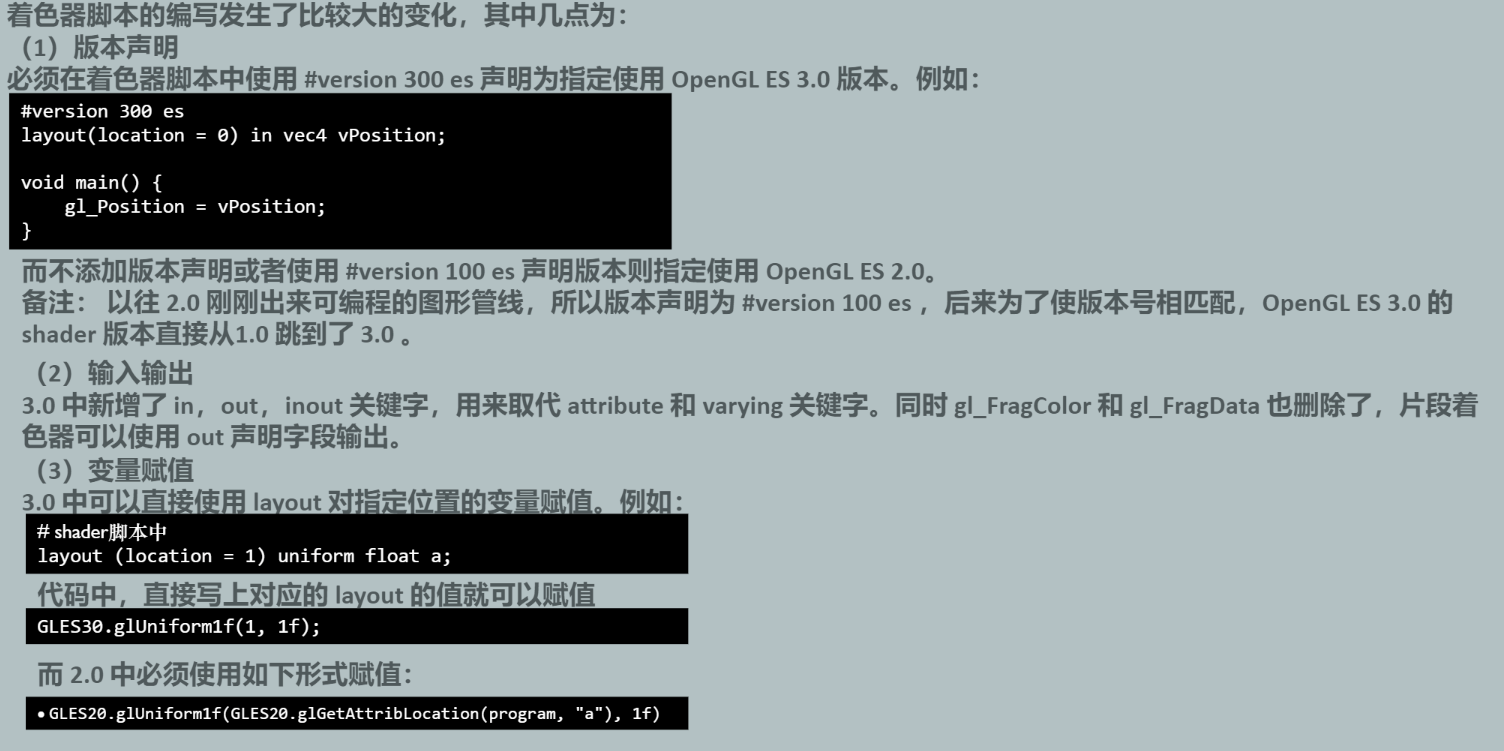
着色器脚本编写