技术美术百人计划学习笔记（图形2.7 Bump图）

1 Bump Mapping 凹凸映射

1.1 表达物体细节的三个尺度

• 宏观尺度
  • 覆盖很多个像素
  • 由顶点或三角形或其他的图元来表示的，建模通常就是在宏观尺度上进行处理
• 中观尺度
  • 覆盖几个像素
  • 描述了宏观尺度和微观尺度之间的特征，细节比较复杂，没有办法使用单个三角形来进行渲染，但这些细节又足够大，能够让观察者看出其中的细节，比如：皮肤的褶皱，肌肉组织的细节，砖块之间的缝隙等等。
• 微观尺度
  • 小于一个像素
  • 表现在着色模型中，而着色模型通常在像素着色器中实现。使用纹理贴图作为参数，模拟物体表面围观几何形状的相互作用，比如高光部分在微观尺度下是光滑的，漫反射部分在微观尺度下是粗糙的

1.2 凹凸映射

• 凹凸映射就是模拟中观尺度的常用方法之一，它能让观察者感知到比几何模型的尺度更小的细节。
• 基本思想是将尺度细节相关的信息编码进纹理中，在着色过程中，我们用稍微受到干扰的表面去模拟真实的表面，从而模拟出表面的小尺度的细节。
• 从原理上讲，凹凸贴图映射技术是对物体表面贴图进行变化，然后再进行光照计算的一种技术。例如给法线分量增加噪音，或者在一个保持扰动值的纹理图中进行查找（视差映射贴图，或者浮雕贴图）
• 这是一种提升物体真实感的有效方法，但却不需要额外的提升物体的几何复杂度（不需要添加额外的顶点）。这种方式在提升物体的表面细节或者表面的不规则性方面有显著效果。

1.3 凹凸映射的分类

• Bump Mapping的种类主要有：法线映射、视差映射、浮雕映射
• 用处广泛，可以用来增加模型细节效果，或者做一些特殊的画面表现效果
• 最常用的是法线映射，一般的增加法线贴图后，会对局部的物体表面进行法线扰动，进而改变明暗关系，从而达到增加表面细节的效果。
• 上述的三种映射都会用到法线贴图

2 Normal Mapping 法线映射

2.1 法线贴图

• Normal Map 是一张存有物体局部表面法线信息的一张贴图。在计算光照的时候，程序会去读取法线图，并获取到当前像素点的法线信息，结合光线信息进行光照计算。
• 使用法线贴图计算光照，可以让物体表现出更加丰富的细节（小范围的明暗变化），并随着光照方向的变换实时变化。
• 法线贴图一般由高模映射到对应的底模上来生成。但像金属，木头等这些细节丰富的物体，可借助程序化的软件如：Photo Shop，Substance Designer等生成

2.2 切线空间

• 法线的存储，一般会放到模型的切线空间中。

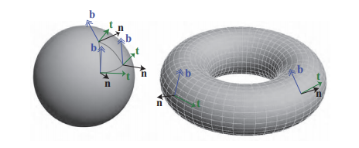
• 切线空间是以物体表面的切线，副切线和法线组成的几何空间

  • 切线空间中，坐标原点为顶点位置，顶点法线$\vec{n}$作为z轴，切线$\vec{t}$和纹理坐标系一致，副切线$\vec{b}$则由顶点法线和切线叉乘得到

    

• 计算光照时，需要把光照运算的向量放到统一坐标系下。读取切线空间法线，需要世界坐标转切线空间的转换矩阵 或 切线空间转世界空间的转换矩阵，将向量统一到同一坐标系后再进行光照操作。

2.3 世界空间和切线空间的转换 —— TBN矩阵

将世界坐标系下的顶点法线（Normal）和切线（Tangent）以及副切线（Bitangent）作为切线空间坐标系的正交基。并用这三个向量的标准正交基来构建转换矩阵。对应关系为法线作为Z轴，切线作为X轴，副切线作为Y轴。

构建一个3*3的矩阵来做空间向量的坐标系转换。一般的叫该矩阵为TBN矩阵。

切线空间→法线空间

在Unity中，将读取到的切线空间的法线信息右乘TBN矩阵，即可将法线从切线空间转换到世界空间

float3x3 TBN = float3x3(i.tangentDir, i.biTangentDir, i.normalDir)
float3 worldNormal = normalize(mul(localNormal, TBN));

世界空间→切线空间

因为TBN矩阵实际上是一个旋转矩阵，而旋转矩阵是一个正交矩阵，所以TBN矩阵的逆矩阵就是TBN的转置矩阵

从世界空间转换到法线空间进行相关处理，只需要顶点右乘TBN矩阵的转置矩阵即可

转换完成后，就可以在相应空间中进行相关着色模型的计算处理

2.4 引入切线空间的好处

实际上法线存在哪个空间下都是可以的，但是实际上我们不仅仅要存储法线信息，更重要的是后续的光照计算。选择哪个坐标系意味着我们需要把光照计算用到的不同信息全部转换到对应的坐标系中。但是，使用切线空间存储法线带来的收益高过空间转换的成本。

优势：

• 自由度高

  • 同一张法线可以作用于不同的模型

  • 如果把法线信息存在模型空间下，得到的则是一个绝对的法线信息，这个法线信息就只是属于一个模型的法线，比如说存到下面球的模型空间下，法线就无法用于右侧的圆环中

    

• 很方便实现UV动画

  • 法线在切线空间中，只是对现有现有法线的扰动。对贴图采样进行偏移时，就可以改动顶点UV实现不同的凹凸效果，进而实现uv动画。（试想一下，如果是在模型空间下，

• 基于同样的原理，可以重用法线贴图

  • 一个立方体一面的法线贴图可以同时用在其他五个面上

• 便于压缩

  • 在切线空间中，法线始终是垂直于表面向外。在归一化的法线向量中，他的值始终是处于0-1之间的，这样的话我们就只用存储副切线和切线，再用sqrt算出法线即可
  • 而在模型空间中，法线可以为负，在-1到1之间，这样就不能通过只存储两个值来推导出法线的值，必须要储存三个值（否则无法指明法线的方向，因为作为贴图的颜色通道，只能存0-1的值），这样就无法压缩了。

2.5 Unity中的法线贴图的压缩格式

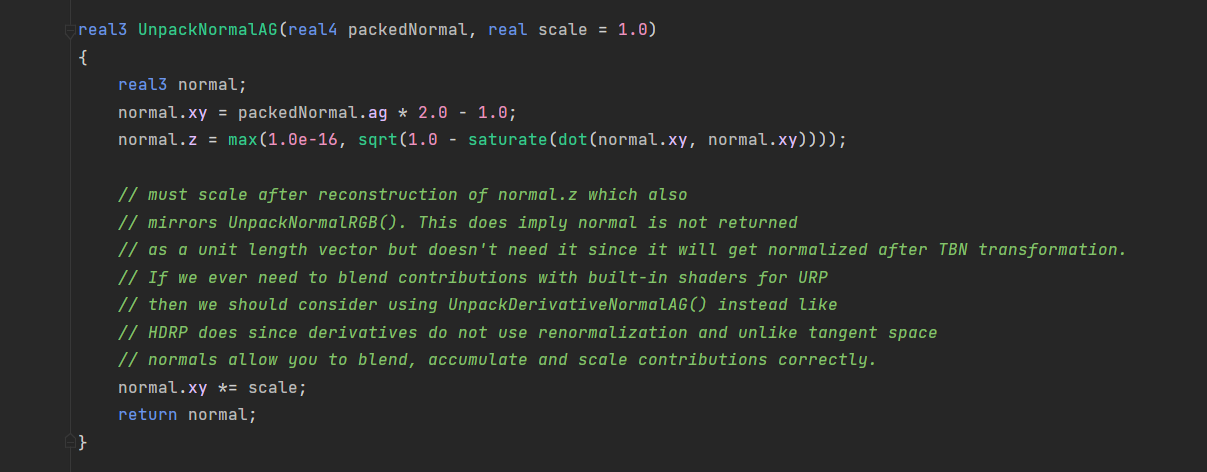
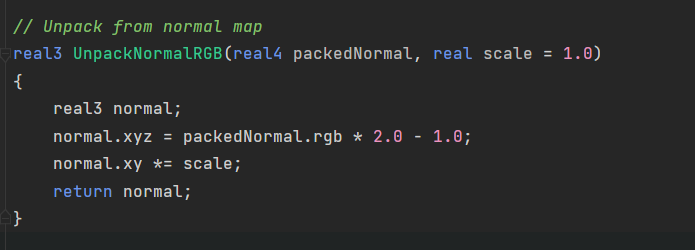
• 在unity中，非移动平台上，Unity会把法线贴图转换成DXRT5nm格式。这种格式只有两个有效通道GA通道，这样可以节省空间
  • GA存储对应法线的y、x分量，z分量需要通过一个简单的运算求得。
• 而移动平台Unity使用传统的RGB通道

3 Parallax Mapping 视差映射

3.1 视差映射的概述

• 视差贴图主要用于赋予物体表面细节遮挡关系，和法线一起使用，能让效果更加逼真
• 视差贴图引入一张新的贴图：高度图
  • 高度图一般是作为顶点位移时使用的，但是模型需要包含大量的三角形才能获得比较不错的效果，否则看起来会成块状。所以如何在有限的三角面上表示令人信服的效果？这就时视差映射技术
  • 视差映射技术核心是改变纹理坐标，但如何改变？怎么改变？这时需要一张存储模型信息的高度图，利用模型表面高度信息来对纹理进行偏移
• 视角越斜，效果越明显

3.2 视差映射的原理

• 视差映射主要是要让平面看起来更立体，和法线贴图一样，是欺骗眼睛的做法

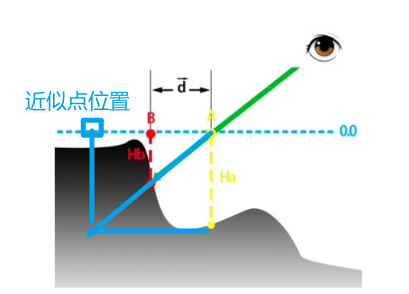
图中蓝色的线0.0为模型表面，正常情况下，我们看到的点A对应的点是黄色的线Ha对应下去的点，当但是如果我们要实现图中灰色部分那样的效果的话，我们实际看到的是B点（红色的线Hb）对应下去的点。

现在的问题是，已知A点的UV，要怎样让他（近似）采样到B点（获得B点或近似B点的UV值）？

• 首先明确一点，是在改一个顶点的UV坐标值，所以说是可以知道视角和模型表面（和法线）之间的夹角的。明白这一点之后就方便理解了。

• 我们可以通过模型表面法线和视线方向的夹角的sin乘上这个点的高度值，这样就能获得uv坐标偏移的算术平方和，进而获得uv偏移值。

  

• 然后用新的uv值去采样A点即可

视差贴图只是一种近似的模拟方法

• 由上图可以看出，实际A偏移后获得的uv坐标与B点还是有比较大的差距的
• 视差贴图的思想理念在于：深度高的地方更容易被遮挡，偏移的值更大；而对于深度小的点来说，更不容易被遮住，所以偏移的值更小；没有深度的点则不做偏移。
• ps：深度图越浅的地方值越小（看上去越黑），越深的地方值越大（看上去越白）

3.3 Steep Parallax Mapping 陡峭视差映射

陡峭视差映射也是一个近似的解，但相比于普通的视差映射要精确很多，效果上也更好，并且会对uv坐标进行合理性检查。

陡峭视差映射的基本思想是将深度分为等距的若干层，然后从最顶层进行采样，并且每次沿着视角方向偏移一定值，若当前层的深度大于采样出的深度，则停止检查并返回最后的结果。

陡峭视差映射解释：

如上图所示，获得A点视线和法线的夹角，用于计算步进长度。一开始时，采样深度是0.25，视线深度是0.0，则向前步进；直到0.5-0.75区间时，发现当前视线深度对应的点D的采样深度为0.5，是第一个采样深度<视线深度的点，那么就认为当前采样的点就是偏移后的点

陡峭视差映射缺点：

问题在于他的分层机制，如果分的层数过多，步进次数会变多，那么性能开销就会比较大；如果分的层数太少，那么就会有明显的锯齿

优化：可以根据视线v和法线n的角度来做对采样层数的最大值和最小值的阈值的限定

4 Relief Mapping 浮雕映射

4.1 浮雕映射的概述

浮雕映射是陡峭视差映射的一个改良版本

浮雕映射相比于视差映射，能够更精确地计算uv偏移量，更容易提供更多的深度，还可以做自阴影以及闭塞效果

4.2 浮雕映射的原理

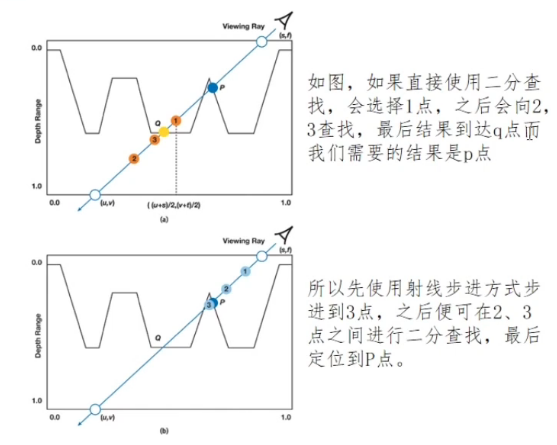
浮雕映射一般先使用射线步进，再使用二分查找的方法来决定UV偏移量

为什么不直接使用二分查找呢：

4.3 陡峭视差映射另外的改良版本 —— 视差闭塞贴图POM

——主要为了解决浮雕贴图映射最后二分查找的性能问题（可能需要迭代多次）

POM相对于浮雕映射贴图，他将二分查找替换成了插值计算，在得到目标区间后，他会对目标区间的两个端点进行采样，通过得到的两个高度值去算数alpha，最终插值得到uv偏移值

（因为用了插值，所以要求凹凸部分要相对平滑）