技术美术百人计划学习笔记（图形5.1.1 基于物理的光照模型）

PBR框架概述

PBR框架包括：

• 基于物理的材质（光照模型）
• 基于物理的灯光
• 基于物理的相机
• 以及美术的PBR全流程。

PBR背后更重要的是PBR带来的框架理念：轻松地利用一个框架去保证项目的整体画面统一

“基于物理”是对现实世界的近似，需要满足三个条件：

• 基于微平面（Microfacet）的表面模型
• 能量守恒
• 应用基于物理的BRDF

微平面理论

概念：将物体表面建模成做无数微观尺度上有随机朝向的理想镜面反射的小平面（microfacet）的理论

能量守恒

概念：出射光线的能量永远不能大于入射光线的能量

表现：随着粗糙度的上升，镜面反射区域的面积会增加，作为平衡，镜面反射区域的平均亮度则会下降

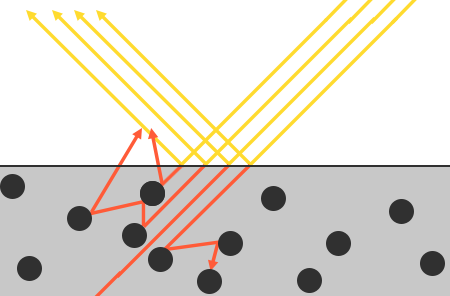
如何能量守恒

简单理解就是：

反射光的强度 = 入射光的强度 * 反射比例 + 入射光的衰减

最终出射光的强度 = 反射光的强度 + 自发光的强度

入射光的衰减 = 半角向量和法线的点积

【唯一的难点就是知道反射比例是多少】

BRDF – 计算反射比例

Bidirectional Reflectance Distribution Function，双向反射分布函数。“双向”意为相机方向和光源方向调换之后，他们所计算出来的能量等级是一致的

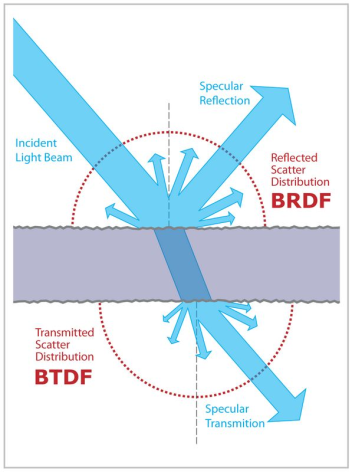
BTDF：双向透射分布函数，用于描述光线透过物体的表现，其也是包含高光反射和漫反射

BSDF = BRDF + BTDF（BSDF双向散射分布函数）

BRDF

BRDF函数作用是：通过入射光的方向和出射光的方向，得到反射比例

应用基于物理的BRDF

BRDF的计算

一般将反射拆分为漫反射和高光反射：

漫反射

算法基本采用Lambert光照模型（经验模型）

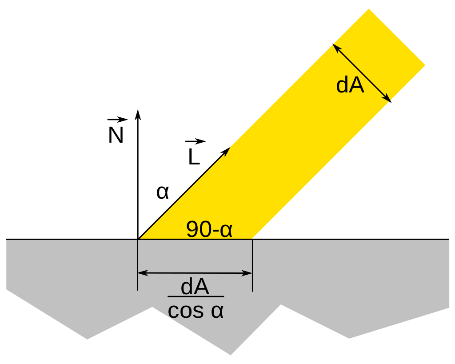
• Kd：漫反射系数，与高光反射系数Ks加和为1
• （I / r ^2）：描述光线能量的衰减

高光反射

• 经验模型

  • Phong模型

  • Blinn-Phong模型

• 基于物理的高光反射：Cook-Torrance反射率方程

D：NDF法线分布函数

“Normal Distrubution Function”

GGX算法：更接近于物理

此处使用的是Trowbridge-Reitz GGX法线分布函数

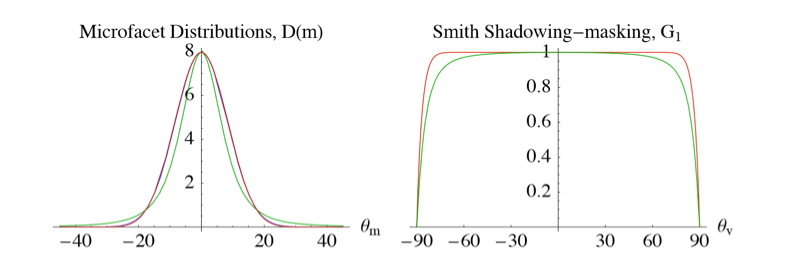
G：几何遮蔽函数

我们使用的微平面理论每个面的计算是互不干扰的，但实际中物体表面凹凸存在相互遮蔽的情况。

因此，几何函数从统计学上近似的求得了微平面间相互遮蔽的比率。这种相互遮蔽会损耗光线的能量。（除了被吸收，还有被自身遮蔽带来的能量损耗）

传统的几何项模型中，需要考虑光线方向和视线方向两种情况的遮蔽效应，所以最终写为：

使用史密斯法与Schlick-GGX作为Gsub可以得到如下所示不同粗糙度的视觉效果

F：菲涅尔方程

被反射的光线对比光线被折射的部分所占的比率（物体的边缘的更亮一些）

总结

BRDF的核心算法是Cook-Torrance反射率方程

漫反射：Lambert

D：

G：

F：

URP中的PBR

Specular工作流的高光颜色由Specular Map控制；而Metallic工作流的高光颜色与Base Color相同

直接看源码就好，顺着URP默认材质的Pass，找到Lit.shader和Lighting.hlsl研究就行

迪士尼原则的BRDF

• 使用直观的参数，而不是物理类的晦涩参数
• 参数应尽可能少
• 参数在其合理范围内应该为0到1
• 允许参数在有意义时超出正常的合理范围
• 所有参数组合应尽可能健壮和合理